Floquet Dynamics

Controlling Quantum Systems with Light: Floquet Engineering in Cavity and Optomechanical Platforms

These two papers explore a shared idea in modern quantum physics: using driven light–matter systems to engineer new kinds of quantum behavior. Instead of studying systems in equilibrium, they examine what happens when cavities or optomechanical setups are continuously driven in time—and how this driving can be used as a control knob for quantum dynamics.

A key concept is Floquet engineering, where periodic driving reshapes a system’s effective behavior. By modulating parameters such as optical fields or coupling strengths, one can create interactions that do not naturally exist in the static system. This allows researchers to simulate or stabilize complex quantum effects using relatively simple physical hardware.

In these systems, light is not just a probe—it actively reshapes the quantum environment. Through carefully designed driving, the system can behave as if it is coupled to an engineered (synthetic) reservoir, which can cool, stabilize, or steer quantum states toward desired targets. This provides a powerful way to control both coherent dynamics and dissipation.

A central result across these works is that time-dependent control can replace hardware complexity. Instead of building strong nonlinearities directly into a device, periodic driving can generate equivalent effective interactions dynamically. This includes directional transport, engineered dissipation, and state stabilization.

Why does this matter?

This approach is important because many quantum technologies rely on fragile states that are hard to control and maintain. Floquet and reservoir engineering offer a scalable alternative: use simple physical platforms plus smart driving protocols to achieve complex quantum functionality.

This could enable:

• scalable quantum simulators using photonic or optomechanical systems
• robust quantum memories stabilized by engineered dissipation
• controllable interfaces between light and matter for quantum networks

More broadly, these works highlight a shift in quantum engineering: instead of fighting noise and dissipation, one can design them to be useful.

In short, these papers show that carefully structured driving of quantum optical systems turns time itself into a tool for designing quantum behavior, enabling flexible control over interactions and quantum states without requiring fundamentally new hardware.

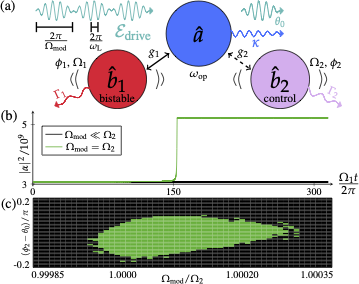
During my PhD I studied the backaction of optomechanical systems under periodic intensity modulation, which lead to a periodic Hamiltonian. It enables the mechanical modes to trigger the instability of another mechanical mode. In the blue detuned regime, it is possible to attain mode-locked lasing of two modes even though there is mode competition which was shown experimentally in (Mercadé et al., 2021). The theoretical formalism shows, that the intensity modulation needs to occur at the difference frequency of the two mechanical oscillators. There is a wonderful intuition that explains the physics of this system in terms of a choir as shown in the figure below.

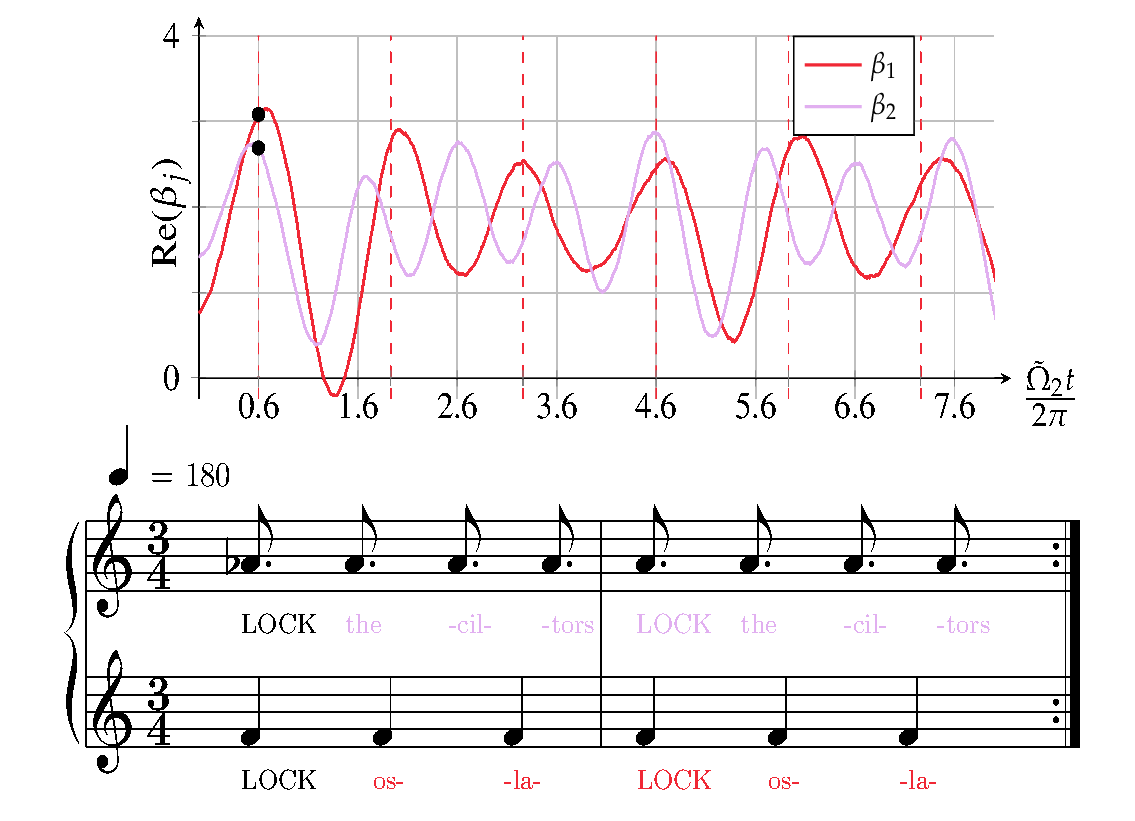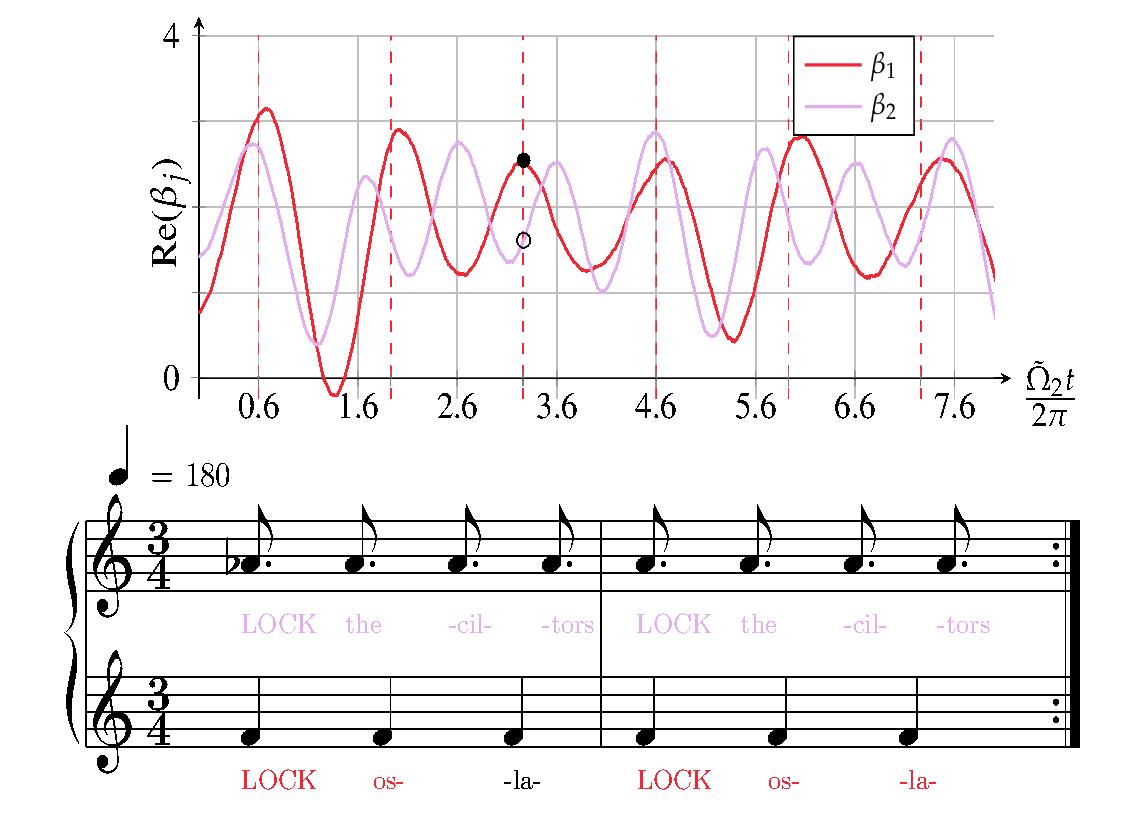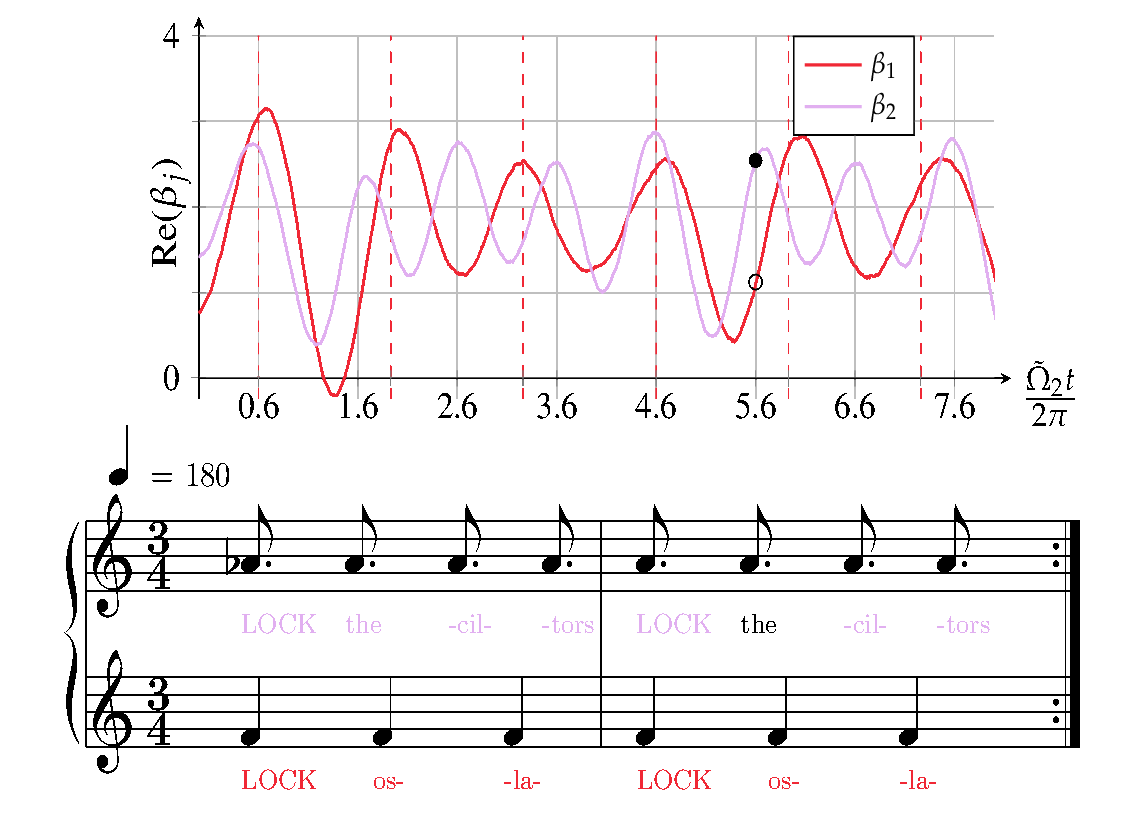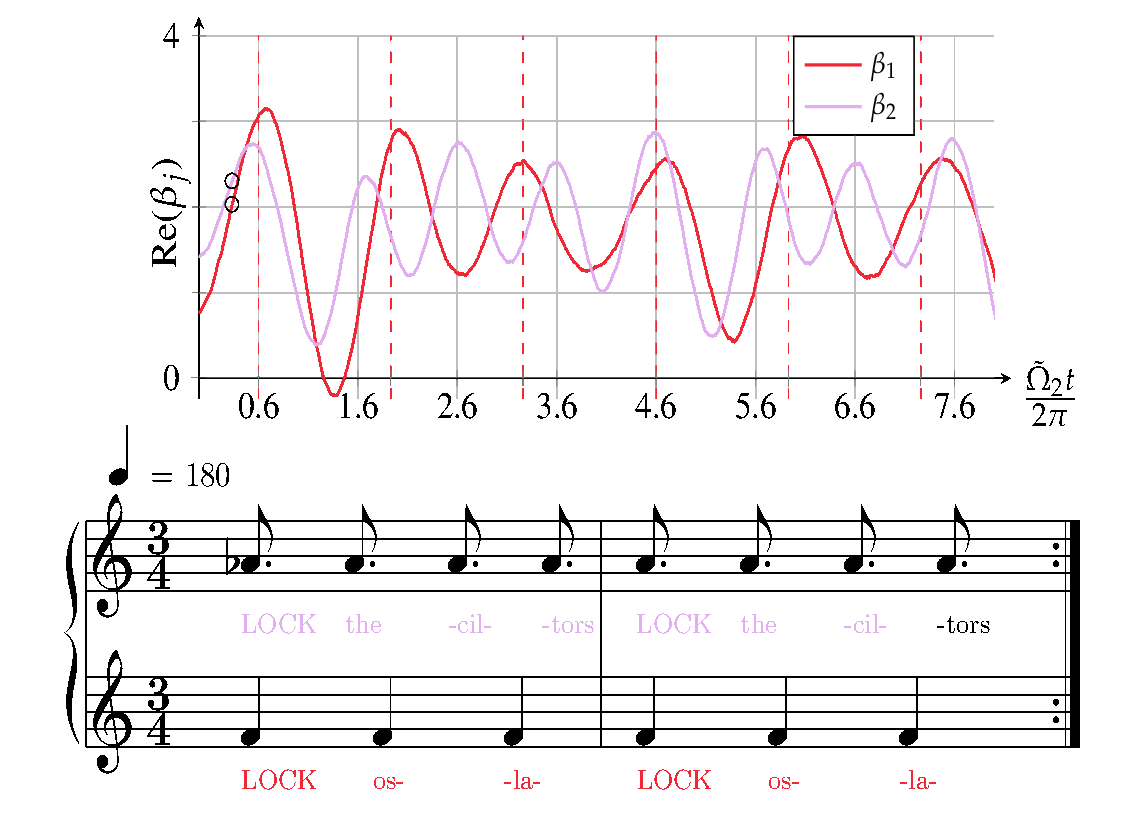
Imagine two groups singing a 4/3 polyrhythm such that the upper group sings notes at a frequency of 4 Hz whilst the other group in the lower line of the clave sings notes at a frequency of 3 Hz. A conductor would indicate the 1 of each measure at a frequency of 1 Hz which happens to be the difference frequency of the two groups.

Employing the same formalism it is also possible to have one mechanical mode trigger the instability—optomechanical bistability in this case—of the other mechanical mode which is published in (Pelka et al., 2022).